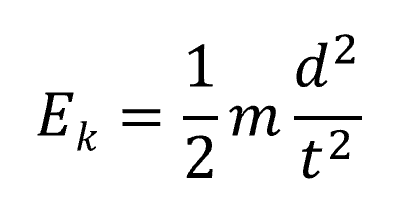Atomic Structure can be split into the following sections:

• Fundamental Particles

• Mass Number and Isotopes

• Mass Spectrometry Method

• Mass Spectrometry Calculation

• Electron Configuration

Fundamental Particles

The model of the atom has changed during modern history and has moved from Dalton’s Billiard Ball to Schrodinger’s model.

Daltons Billiard ball is a solid uncharged sphere which was used until the discovery of the electron by JJ Thompson.

The discovery of the electron led to the development of the plum pudding model which is a sphere of positive charge with negatively charged electrons scattered within it. Moving forward in time Ernest Rutherford gold foil experiment proved the existence of the nucleus so the model had to then change.

The nuclear model was then created with electrons orbiting a nucleus. This was then further improved by Niels Bohr who put the electrons in discreet shells.

After the Bohr Model there was further development in quantum physics which used Schrodinger’s waveform equations to produce orbitals. We will discuss these more later.

The subatomic particles have the following relative charges and masses.

To calculate the mass of one subatomic particle divide the relative mass by Avagadro’s Number.

Mass Number and Isotopes

Relative Atomic Mass is the average mass of the naturaly occurring atoms of an element compared to one twelfth of the mass of carbon-12. The relative atomic mass of an atom is calculated by adding the number of protons to the number of neutrons, the amount of electrons is negligible. Conversely the amount of neutrons can be calculated by the total atomic mass minus the proton number.

Isotopes are atoms of the same element, they have the same proton number, but have a different number of neutrons. The isotopes are used with their relative abundance to calculate the relative atomic mass.

Calculating Relative Atomic Mass

The most common question involving relative atomic mass is simply calculating using a table of values, below is an example.

To calculate the relative abundance of boron we use the equation Sum(Isotope mass x Relative abundance)= Relative Atomic Mass.

10*0.199+11*0.801=10.801.

Mass Spectrometry

Mass spectrometry is a technique used to obtain a mass to charge ratio (m/z), this is generally read as mass as most samples ionised will have a charge of +1. There is iver main sections of a mass spectrometer.

Ionisation – This is done with one of two methods, the first being electron bombardment. In electron bombardments the sample is first injected and vapourised in an ionisation chamber, in this chamber the sample is subjected to high energy electrons, these high energy electrons will remove an electron from the sample molecule/atom.

The second method of ionisation is electrospray, the sample is dissolved in solvent and injected in to the ionisation chamber, the needle is given a high positive potential difference which causes the solvent and sample to vapourise. Once the sample vapourises it will take a proton with the sample producing a charged particle of mass +1. The m/z value from the output will need to be reduced by 1 to account for this proton.

Acceleration – After ionisation the positive ion is accelerated towards a negatively charged plate, each ion will receive the same amount of force/energy so the smaller the ion the faster it will accelerate and be at a higher speed at the end of acceleration.

Drift  - Once the ions have been accelerated they are traveling at speeds relative to their mass they then pass in to a flight tube in order to separate from each other, a flight tube is typically 1-2m long. Acceleration and drift must occur in a vacuum to avoid collisions.

Detection – Ions reach the detector at different times due to traveling at different speeds. When the ion hits the detector the ions take an electron from it.

The detector losing a charged particle generates a current, the size of the current is proportional to the abundance of the ion. The more ions of the same mass produces a higher current at a specific time.

Data Analysis – The data from the detector is fed in to a computer which converts the signal in to relative abundances of mass to charge ratio (m/z).

·       Mass Spectrometry Calculations

The mass of an ion can be calculated using its speed by using a combination of the following equations.

Combined they become the following,

v = velocity (m/s)

d = distance (m)

t = time (s)

ke = kinetic energy (j)

m = mass (kg)

Question: Sample X is injected in to a TOF mass spectrometer with an electron bombardment ionisation chamber. Each ion is accelerated with the same energy of 1.48x10^-16J. The length of the light tube is 1.2m and takes 4.32 x10^-5s. Calculate the mass in g of the ion.

First we must calculate the velocity of the ion. v = d/t.

1.2/4.32x10^-5= 27777m/s

We then need to re-arange the second equation to make the mass the subject and then substitute in to it.

Ke = 1/2mv^2

m = 2KE/v^2

m= 2x1.48x10^-16J/27777m/s^2 = 3.836x10-27kg

Then convert kg to g by x by 1000.

3.836x10-27 kg = 3.836x10-24 g

More calculations will be added soon.

Ionisation energies and electron configuration

 Electron Configuration

Electron configuration is how the electrons are arranged for an atom, It is usually done in the ground state, this means the atom has the lowest possible energy levels occupied. The Aufbau principle is used where electrons are put in to the lowest possible energy level or orbital, two ways of describing the same thing.

The above graph can be use for explain both first ionisation energy and writing electron structures. First ionisation energy is the enthalpy change required to remove one mole of electrons from one moles of gaseous atoms. We are therefore trying to remove an electron when ionising.

On the graph  below we can see that the highest occupied energy level is 2p, the amount of energy which is required to remove the electron from the atom, from one of those 2p orbitals is the first ionisation energy.

Ionisation energy generally increases as we go across the periodic table due an increased nuclear charge, decreased atomic radius, and identical shielding which increases the force of attraction between the nucleus and outer shell electron. There is exceptions to this explained below. Ionisation energy will decrease as we go down a group as there is an increased amount of shielding and increased atomic radius which will reduce the attraction between the nucleus and the outer shell electron. This means helium has the highest first ionisation energy and francium the lowest.

The second ionisation energy is the enthalpy change of removing one moles of electrons from one mole of gaseous +1 ions.

The second ionisation energy is always higher than the first ionisation energy as a negative ion is being removed from a positive ion and therefore has an electrostatic force of attraction, the electron may also be in a lower energy level, 3s compared to 3p, which also requires a greater amount of energy.

The above graph shows the shells, sub sells and orbitals. A shell if what is learnt at GCSE and the graph above shows 3 shells, 1,2, and 3. Shells are then divided in to up to 4 subshells, they are also referenced on the periodic table, of s, p, d, and f.

Shell 1 contains an s sub shell

Shell 2 contains an s sub shell and a p sub shell

Shell 3 contains an s sub shells, a p subshell and a d sub shell

The 4th shell contains s, p, d, and f subshells but is beyond the A-level course.

Each sub shell is then divided in to orbitals, each of these contain a pair of electrons.

The s subshell contains one orbital.

The p subshell contains 3 orbitals.

The d subshell contains 5 orbitals.

The f subshell contains 7 orbitals.

The periodic table is split in to 4 sections, s-block, p-block, d-block, and f-block, the block indicates the highest energy level subshell of the atom.

Writing electronic structures

For example if we are to write the electronic structure of sulfur, first we need to use the periodic table and recognise that a sulfur atom has 16 electrons so would fill the graph as below.

The electronic structure for sulfur is written in full or as short hand where the noble gas from the previous period is used and then only the electrons after that are written

The super script indicates how many electrons are in each subshell, which is stated prior to the subscript.

The 3d subshell is higher in energy than the 4s subshell so the 4s subshell will fill before the 3d subshell so for example the electron structure for Iron,

Exceptions Cr & Cu are slightly different, a half filled or completely filled d subshell gives the atom an increased level of stability so they will take one of the electrons from the s subshell to achieve this which gives the following electron structures

Electronic Structures of ions

When electrons are lost from atoms the outer most electron is lost, not the highest energy level. When removing electrons from elements with 4s and 3d subshells with electrons, the 4s electrons are removed first, not the 3d electrons.

Ionisation energies and evidence of orbitals.

As explained above going across the periodic table there is an increase in first ionisation energy, if we look at period 3 there is two instances where the first ionisation energy decreases as we go across the period.

Mg to Al has a decrease in first ionisation energy, this is because the electron removed in Al is in the p subshell which is a higher energy level than the s subshell so requires less energy to remove.

P to S has a decrease in first ionisation energy as the electron removed is from a full orbital, the full orbital contains 2 electrons which are repelling each other so require less energy to remove.